Pricing

Introduce the exact and efficient quantative methods to price the derivatives from A to Z.

VS2019에서 PyTorch C++ 환경설정
1. Pythorch 다운로드
2. VS2019 프로젝트 환경 설정
PyTorch를 이용한 Black-Scholes 가격 계산

VS2019에서 PyTorch C++ 환경설정

Pythorch 다운로드

www.pytorch.org 에서 libtorch 압축파일을 다운로드 받고, 압축을 푼다.
CUDA 버전과 CPU-only 버전에 따라 다른 파일을 다운로드함.
CUDA10 을 사용하는 경우 다운로드 경로는 다음과 같다.
Download here (Release version)
Download here (Debug version)

VS2019 프로젝트 환경 설정

VC++ 디렉터리
- 포함 디렉터리 에 다음의 2개의 include 경로를 추가함
  <압축해제 디렉토리 경로명>\libtorch\include
  <압축해제 디렉토리 경로명>\libtorch\include\torch\csrc\api\include
- 라이브러리 디렉터리 에 다음의 lib 경로를 추가함
  <압축해제 디렉토리 경로명>\libtorch\lib
링커 - 입력
- 추가 종속성 에 다음 lib 파일을 추가
```
   torch.lib
   c10.lib
```
디버깅
- 프로그램 실행을 위해 torch.dll 파일이 필요함
- 디버깅 환경변수에 torch.dll 경로를 추가
  PATH=%PATH%;<압축해제 디렉토리 경로>\libtorch\lib

PyTorch를 이용한 Black-Scholes 가격 계산

PyTorch는 딥러닝을 위한 툴이지만, 빠른 벡터(텐서) 연산이 가능하다는 점에서 옵션 평가에 유용하게 활용될 수 있을 것이라고 기대할 수 있다. 특히 계산시간이 중요한 몬테카를로 시뮬레이션을 실행할 때 계산 시간을 현격히 단축시킬수 있다.

간단한 Plain-Vanilla 옵션의 가격과 델타를 몬테카를로 시뮬레이션을 이용해서 계산하고자 한다. 먼저 PyTorch를 이용해서 계산하는 C++ 코드를 작성하고 일반적인 C++ STD를 이용한 싱글코어 프로그램과 성능을 비교하였다(PyTorch C++ API 이용).

__Timer__: 계산시간을 측정하기 위한 클래스(boost를 사용하려다가 인터넷에서 소스코드 가져옴)
__bsprice__: 블랙숄즈 옵션 가격 공식을 이용해서 가격과 델타를 계산하는 함수

#pragma warning(disable:4251 4275 4244 4267 4522 4273 4018 4305)
#include <torch/torch.h>
#include <cmath>
#include <cstdio>
#include <iostream>
#include <ctime>
#include <chrono>
#include <random>
#define MAX(x,y) (((x)>(y)) ? (x) : (y))

class Timer {
public:
	Timer() : beg_(clock_::now()) {}
	void reset() { beg_ = clock_::now(); }
	double elapsed() const {
		return std::chrono::duration_cast<second_>
			(clock_::now() - beg_).count();
	}
private:
	typedef std::chrono::high_resolution_clock clock_;
	typedef std::chrono::duration<double, std::ratio<1> > second_;
	std::chrono::time_point<clock_> beg_;
};

enum OptionType {
	Call = 1, Put = -1
};

struct PriceResult {
	double price;
	double delta;
};

double normcdf(double x, double mu=0, double sigma=1) {
	double v = (x - mu) / sigma;
	return 0.5 * erfc(-v * M_SQRT1_2);
}

PriceResult bsprice(double s, double k,	double r, double q, double t,
   double sigma, OptionType type) {
	double d1 = (log(s / k) + (r - q + 0.5 * sigma * sigma) * t) / (sigma * sqrt(t));
	double d2 = d1 - sigma * sqrt(t);
	double nd1 = normcdf(type * d1);
	double nd2 = normcdf(type * d2);
	double price = type * (s * exp(-q * t) * nd1 - k * exp(-r * t) * nd2);
	double delta = type * exp(-q * t) * nd1;
	return PriceResult({ price, delta });
}

__mcprice_cpu__: 싱글코어에서 몬테카를로 시뮬레이션으로 옵션 가격과 델타를 계산하는 함수
- std::mt19937_64 를 이용해 random number를 생성
- std::normal_distribution 을 이용해서 정규분포를 따르는 난수

PriceResult mcprice_cpu(double s, double k, double r, double q, double t, 
  double sigma, OptionType type, unsigned int ntimes, unsigned int numOfSimulation) {
	double sumOfPayoff = 0, sumOfDelta = 0;
	double df = exp(-r * t);
	std::mt19937_64 gen;
	std::normal_distribution<double> engine(0.0, 1.0);
	gen.seed(std::random_device{}());
	double dt = t / ntimes;
	double es = exp((r - q - 0.5 * sigma * sigma) * dt);
	double diffution = sigma * sqrt(dt);
	for (unsigned int i = 0; i < numOfSimulation; ++i) {
		double st = s;
		for (unsigned int j = 0; j < ntimes; ++j) {
			double e = engine(gen);
			st = st * es * exp(diffution * e);
		}
		double p = MAX(type * (st - k), 0);
		double d = type * (st - k) > 0 ? type * st / s : 0;
		sumOfPayoff += df * p;
		sumOfDelta += df * d;
	}
	double price = sumOfPayoff / numOfSimulation;
	double delta = sumOfDelta / numOfSimulation;
	return PriceResult({ price, delta });
}

mcprice_torch: PyTorch Tensor를 이용한 가격 계산 함수, CUDA를 사용가능한 경우 device는 CUDA를 사용할 수 있도록 함

PriceResult mcprice_torch(double s0, double k, double r, double q, double t,
  double sigma, OptionType type, unsigned int ntimes, unsigned int numOfSimulation) {
	torch::manual_seed(rand());

	// Create the device we pass around based on whether CUDA is available.
	torch::Device device(torch::kCPU);
	if (torch::cuda::is_available()) {
		//std::cout << "CUDA is available! Training on GPU." << std::endl;
		device = torch::Device(torch::kCUDA);
	}

	auto options_0 =
		torch::TensorOptions()
		.dtype(torch::kFloat64)
		.device(device)
		.requires_grad(true);

	auto options_1 =
		torch::TensorOptions()
		.dtype(torch::kFloat64)
		.device(device)
		.requires_grad(false);

	int m = numOfSimulation;

	torch::Tensor s_0 = torch::tensor(s0, options_0);

	double dt = t / ntimes;
	//int ntimes = int(t / dt);
	torch::Tensor ts = torch::arange(0.0, t + dt, dt, options_1);

	torch::Tensor e = torch::randn({ m, ntimes }, options_1);
	torch::Tensor sum_e = torch::cumsum(e, 1);	
	sum_e = torch::cat({ torch::zeros({ m, 1 }, options_1), sum_e }, 1);
	torch::Tensor s = s_0 * torch::exp((r - q - 0.5 * sigma * sigma) * ts + sigma * sqrt(dt) * sum_e);

	double disc = exp(-r * t);
	auto sAtMat = s.index({ torch::arange(0, s.size(0), torch::kLong), torch::tensor(s.size(1) - 1) });
	torch::Tensor discPayoff = disc * torch::relu(type *( sAtMat - k));
	auto price = discPayoff.mean();
	price.backward();
	return PriceResult({ price.item<double>(), s_0.grad().item<double>() });
}

__main__ 함수:
- 시뮬레이션 Path 생성 회수 = 50,000번
- Path당 time step의 개수 = 100개(Plain-vanilla 옵션의 평가는 만기일 이전에 time node가 불필요하지만 계산 성능 비교를 위해 100개의 time step을 가정함)
- PyTorch를 이용한 가격 계산은 10회 반복하여 계산(첫번째 실행에는 GPU 초기화를 위해 상당 시간을 소모하여 2회 이상 실행이 필요함)

int main(int argc, const char* argv[]) {

	Timer tmr;
	double s = 100, k = 100, r = 0.02, q = 0.01, t = 0.25, sigma = 0.15;
	OptionType type = Call;
	unsigned int ntimes = 100, numOfSimulation = 50000;

	std::cout << "Pricing with BS Formula" << std::endl;
	tmr.reset();
	PriceResult res_anal = bsprice(s, k, r, q, t, sigma, type);	
	std::cout << "Anal Price = " << res_anal.price << "\t";
	std::cout << "Delta = " << res_anal.delta << std::endl;
	std::cout << std::string(40, '-') << std::endl;
		
	tmr.reset();
	std::cout << "Pricing with STD" << std::endl;
	PriceResult res_std = mcprice_cpu(s, k, r, q, t, sigma, type, ntimes, numOfSimulation);
	double computationTime = tmr.elapsed();
	std::cout << "MC Price = " << res_std.price << "\t";

	std::cout << "Delta = " << res_std.delta << std::endl;
	std::cout << "Time = " << computationTime << std::endl;
	std::cout << std::string(40, '-') << std::endl;

	
	for (int _i = 0; _i < 10; _i++) {
		tmr.reset();		
		std::cout << "Pricing with Torch  #" << _i+1 << std::endl;
		PriceResult res_torch = mcprice_torch(s, k, r, q, t, sigma, type, ntimes, numOfSimulation);
		computationTime = tmr.elapsed();
		std::cout << "MC Price = " << res_torch.price << "\t";
		std::cout << "Delta = " << res_torch.delta << std::endl;
		std::cout << "Time = " << computationTime << std::endl;
		std::cout << std::string(40, '-') << std::endl;
	}	
}

결과

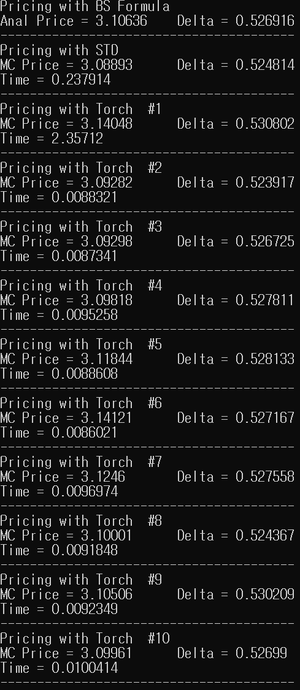
Results

가격과 델타 모두 analytic formula에 의해 계산된 결과와 거의 일치한다.

계산 시간은 싱글코어에서 0.24초 걸린데 반해, CUDA에서는 첫번째 실행 시간은 2.4초 정도로 10배 가량 오래 걸렸지만 이후 실행에서는 대략 0.01초 정도로 20배 이상 빠르게 계산되었다.

프로세서 : Intel(R) Core(TM) i7-9700F CPU @ 3.00GHz, 3000Mhz, 8 코어, 8 논리 프로세서
GPU : NVIDIA GeForce RTX 2060, CUDA v10.1

Back to Table of contents

Pricing

VS2019에서 PyTorch C++ 환경설정

Pythorch 다운로드

VS2019 프로젝트 환경 설정

PyTorch를 이용한 Black-Scholes 가격 계산

Qvious, Inc.

Error

VS2019에서 PyTorch C++ 환경설정

Pythorch 다운로드

VS2019 프로젝트 환경 설정

PyTorch를 이용한 Black-Scholes 가격 계산

Templates (for web app):

Error